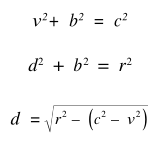在光线追踪器里面,光线-对象的相交运算是计算量最大的,当然也是最重要的。相交计算的效率关系着渲染效率,相交的结果关系着渲染结果。光线-球体相交可能是所有光线-几何体相交中最简单的了,这也是为什么有那么多光线追踪器使用反射球来展示渲染结果。由于其简单性,所以计算速度也快。
本文我们也选择球体来作为渲染对象。对于光线-球体的相交计算,有两种方法。一种基于几何学,另一种利用解析几何(线性代数)。后者是大部分渲染器器采用的方案,原因在于这种方法可以重用于其他各种平面形状。
光线-对象相交计算主要是为了回答是否相交?、相交点在哪?、最近相交点在哪?等问题。然后渲染器对最近相交点做一系列后续操作,比如递归追踪光线、根据材质计算反射值,最后算出该点的颜色值,然后再是过滤采样得到最终像素值,最后成为一张完整的图像。这些操作以后会慢慢涉及到,现在先做光线-球体相交计算。
几何学方案
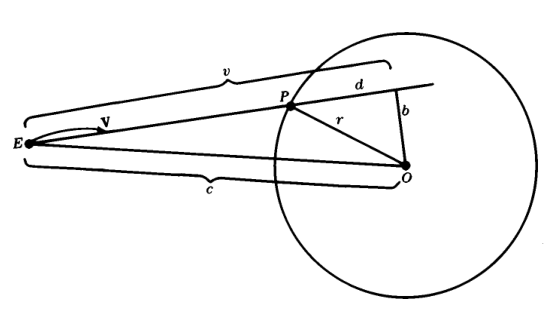
基于几何的方案非常直观,光线就是射线,而球体在平面上就是一个圆,所以问题就成了求射线与圆的交点。射线用向量可以表示成 P(t) = O + tD,O 为起点,D 为方向(一般使用单位向量)。
如图所示:
由图可以得到下面几个等式:
我们需要计算出 P 点位置,那先计算出距离 d,然后由 E + (v-d)V 就可以得到了。当然,在图形学中,这些计算都有依赖于向量计算。最终 P 的位置也是由向量表示的。
设 V 为单位向量,表示光线的方向,E 为光线的起点。伪代码如下:
文末会有C代码实现。
线性代数方案
所谓现行代数,也叫解析几何,即使用代数的方法解决几何学问题,其表现形式多为解高阶方程。求光线与球体的相交点本质上就是求射线与圆的交点。
射线可表示为起点加方向,所以光线的向量形式为 P(t) = O + tD。球体可表示为球心(O)加半径(R),即 (X-Xo)^2 + (Y-Yo)^2 + (Z-Zo)^2 = R^2,用向量形式表示为 (P-C)·(P-C) = R^2。然后我们就可以利用光线和球体的向量形式解方程了。(将光线P代入球体方程就行。)
具体步骤如下:

实现
typedef struct {
Vec3 org, dir;
} Ray;
typedef struct {
Vec3 pos;
double rad;
} Sphere;
double ray_sphere_inter_analytic(Ray *ray, Sphere *sphere)
{
/* Analytic Solution
* return smaller distance, 0.0 refer no hit
*/
Vec3 op;
vsub(op, sphere->pos, ray->org);
double t, epsilon = 1e-4;
double a = vdot(ray->dir, ray->dir);
double b = 2 * vdot(op, ray->dir);
double c = vdot(op, op) - sphere->rad * sphere->rad;
double det = b * b - 4.0 * a * c; /* b^2 - 4ac */
if (det < 0.0)
return 0.0;
else
det = sqrt(det);
return (t = (-b - det) * 0.5 / a) > epsilon ? t : ((t = (-b + det) * 0.5 / a) > epsilon ? t : 0.0);
}
double ray_sphere_inter_geometric(Ray *ray, Sphere *sphere)
{
/* Solution
* return smaller distance, 0.0 refer no hit .
*/
Vec3 op;
vsub(op, sphere->pos, ray->org);
double v = vdot(op, ray->dir);
double det = sphere->rad * sphere->rad - (vdot(op, op) - v * v);
if (det < 0.0)
return 0.0;
else
det = sqrt(det);
return v - det;
}
参考
- 《Graphics Gems I》
- 《Mathematics for 3D Game Programming and Computer Graphics》
- 《An Introduction to Ray Tracing (1989)》